Start / Lineare Funktionen
Inhalt
Koordinatensystem
Was ist eine lineare Funktion?
Was wir direkt aus der Gleichung ablesen können
Den Schnittpunkt zweier Geraden berechnen
Punktprobe
Gleichung aus zwei Punkten aufstellen
Wo wird die x-Achse geschnitten?
Aufgaben
 Koordinatensystem
Koordinatensystem
Ein Koordinatensystem ermöglicht es uns die Position eines Punktes auf einer Fläche zu beschreiben.
Dazu haben wir zwei Achsen, auf denen (wie bei einem Lineal) Skalen angebracht sind. Im folgenden Koordinatensystem sind die Punkte A, B, C, und D eingezeichnet:
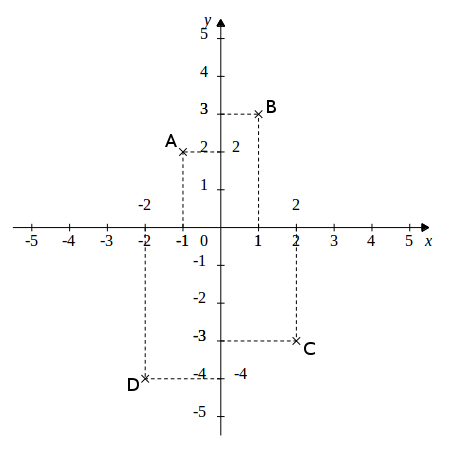
Die Koordinaten werden in folgender Weise angegeben:
(x-Wert|y-Wert)
Der Wert der x-Koordinaten wird immer zuerst genannt (alphabetische Reihenfolge).
Die Koordinaten der Punkte in der Zeichnung lauten also: A(-1|2), B(1|3), C(2|-3) und D(-2|-4)
 Was ist eine lineare Funktion?
Was ist eine lineare Funktion?
Eine Funktion ist eine eindeutige Zuordnung.
So ist zum Beispiel jedem angemeldeten Auto ein amtliches Nummernschild zugeordnet. Diese Zuordnung ist eindeutig, denn das gleiche Nummernschild darf nur von einem Auto verwendet werden.
Ein ähnliches Beispiel sind Städte und ihre Postleitzahlen.
In der Mathematik ordnen wir oft Zahlen andere Zahlen zu.
Die folgende Gleichung ist eine Funktion:
$y=2x-3$
Mit ihrer Hilfe können wir Zahlenpaare $(x|y)$ bilden, indem wir für x eine beliebige Zahl einsetzen und das passende y ausrechnen.
So erhalten wir für $x=1$ $y=2 \cdot 1 -3=-1$ das Zahlenpaar $(1|-1)$.
Lineare Funktionen
Eine lineare Funktion wird durch eine Gleichung des Typs:
$y=mx+b$
ausgedrückt. Anmerkung: Für m und b stehen in einer konkreten Gleichung natürlich Zahlen.
Warum nennen wir eine solche Funktion linear?
Wenn wir für $y=2x-3$ mehrere Wertepaare ausrechnen
$(-1|-5)~~~~~ (0|-3)~~~~~ (1|-1)~~~~~ (2|1)$,
können wir diese Wertepaare als Punkte in einem Koordinatensystem auffassen und einzeichnen.
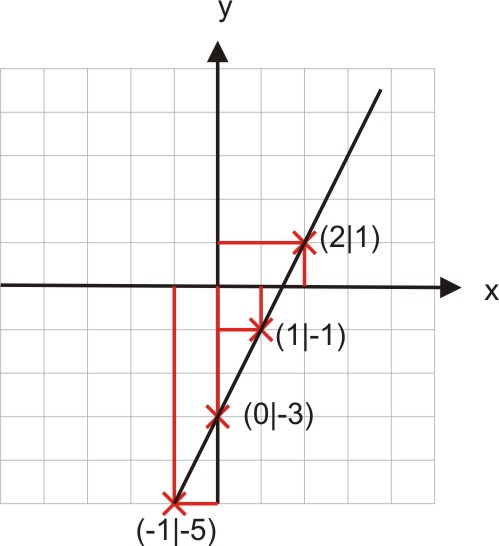
Bei genauerem Hinsehen fällt auf, dass die Punkte auf einer geraden Linie liegen, weshalb wir die Funktion linear nennen.
Tipp
Da eine Gerade durch zwei Punkte eindeutig festgelegt ist, brauchen wir nur zwei Wertepaare auszurechnen, um die Gerade in das Koordinatensystem einzuzeichnen.
Wir können dann die Zeichnung verwenden, um zu anderen x-Werten den passenden y-Wert (oder umgekehrt) abzulesen.
 Was wir direkt aus der Gleichung ablesen können
Was wir direkt aus der Gleichung ablesen können
Betrachten wir die folgenden drei Funktionen des Typs $y=mx+b$:
Rote Gerade: Steil, aufwärts, schneidet y-Achse bei (0|-2)
Gleichung: $y=2x-2$
$m=2~~~~b=-2$
Grüne Gerade: Flach, aufwärts, schneidet y-Achse bei (0|1)
Gleichung: $y=0,5x+1$
$m=0,5~~~~b=1$
Blaue Gerade: Steil, abwärts, schneidet y-Achse bei (0|1)
$y=-2x+1$
$m=-2~~~~b=1$
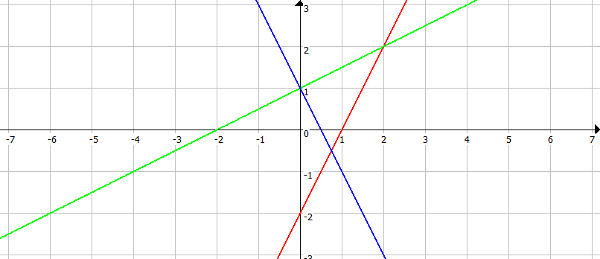
Steigung
Der Wert m drückt aus, welche Steigung unsere Gerade hat. Dabei gilt folgende Regel:
Positives m $m>0$: Die Gerade steigt (In unserem Beispiel: rot und grün).
Negatives m $m<0$: Die Gerade fällt (In unserem Beispiel: blau).
Für $m=0$: Die Gerade ist waagerecht (kommt in unserem Beispiel nicht vor).
Des weiteren gilt:
$|m|>1$: Gerade steigt oder fällt eher steil (In unserem Beispiel: rot und blau).
$|m|<1$: Gerade steigt oder fällt eher flach (In unserem Beispiel: grün).
Schnittpunkt mit der y-Achse
Am Wert von b können wir direkt sehen, wo die y-Achse geschnitten wird. Machen Sie sich das an unserem Beispiel klar.
 Den Schnittpunkt zweier Geraden berechnen
Den Schnittpunkt zweier Geraden berechnen
1. Schritt: Wir fassen die beiden Funktionsgleichungen zu einem Gleichungssystem zusammen.
2. Schritt: Wir versuchen das Gleichungssystem zu lösen.
Ist das Gleichungssystem lösbar, liefert uns die Lösung die x- und die y-Koordinate des Schnittpunktes.
Ist das Gleichungssystem unlösbar, gibt es keinen Schnittpunkt, da die Geraden parallel verlaufen.
Hat das Gleichungssystem unendlich viele Lösungen, sind die beiden Geraden identisch.
 Punktprobe
Punktprobe
Dazu setzen wir die Koordinaten des Punktes in die Funktionsgleichung der Geraden ein. Ist die Gleichung dann noch wahr, liegt der Punkt auf der Geraden. Wird die Gleichung dadurch falsch, liegt der Punkt nicht auf der Geraden.
Beispiel:
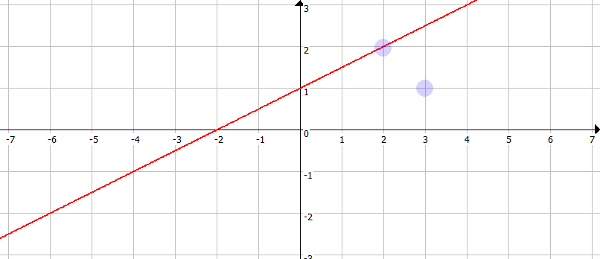
Geradengleichung: $y=0,5x+1$ Punkt1: $(2|2)$ Punkt 2: $(3|1)$
Punkt 1 prüfen:
$2 =^? 0,5 \cdot 2 + 1$
$2 =^? 1 + 1$
$2 = 2$ Der Punkt liegt auf der Geraden (vergl. Zeichnung).
Punkt 2 prüfen:
$1 =^? 0,5 \cdot 3 + 1$
$1 =^? 1,5 + 1$
$1 \not = 2,5$ Der Punkt liegt nicht auf der Geraden (vergl. Zeichnung).
 Gleichung aus zwei Punkten aufstellen
Gleichung aus zwei Punkten aufstellen
Aus den Punkten A(2|3) und B(5|0) soll die Gleichung der Geraden aufgestellt werden, die durch diese beiden Punkte geht.
Methode 1: Aufstellen eines linearen Gleichungsystems
1. Schritt: Wir setzen die Koordinaten von A in die allgemeine Gleichung: $y=mx +b$ ein und erhalten dadurch eine Gleichung mit den Variablen m und b.
2. Schritt: Wir machen das Gleiche mit den Koordinaten des Punktes B.
3. Schritt: Wir lösen das aus den Gleichungen gebildete Gleichungssystem
4. Schritt: Wir setzen die Werte für m und b in die allgemeine Gleichung ein und erhalten die Funktionsgleichung der Geraden.
In der Praxis:
$\begin{matrix} I & 3 & = & 2m + b & ~|~\cdot (-1)\\ II & 0 & = & 5m + b & ~\\ I & -3 & = & -2m - b & ~\\ I+II & -3 & = & 3m & |~: 3\\ ~ & -1 & = & m & ~\\ I & 3 & = & 2 \cdot (-1) + b & ~\\ I & 3 & = & -2 + b & ~|~+2\\ I & 5 & = & b & ~\\ \end{matrix}$
4. Schritt:
$y = -1x + 5$
Methode 2: Verwenden der Zweipunkteform
Die Zweipunkteform lautet:
$$y = \frac{y_2 - y_1}{x_2-x_1}(x-x_1) + y_1$$
In diese Formel setzen wir die Koordinaten der beiden Punkte ein und vereinfachen die Gleichung.
Wie nehmen beispielsweise A(2|3) als ersten und B(5|0) als zweiten Punkt an:
$y = \frac{0 - 3}{5-2}(x-2) + 3$
$y = -1(x-2) + 3$
$y = -1x +2 + 3$
$y = -1x +5$
Dabei ist es unerheblich, welchen Punkt wir als ersten und welchen wir als zweiten annehmen. Wir kommen zum Gleichen Ergebnis, wenn wir B als ersten und A als zweiten Punkt einsetzen:
$y = \frac{3-0}{2-5}(x-5) +0$
$y = -1(x-5) +0$
$y = -1x +5$
 Wo wird die x-Achse geschnitten?
Wo wird die x-Achse geschnitten?
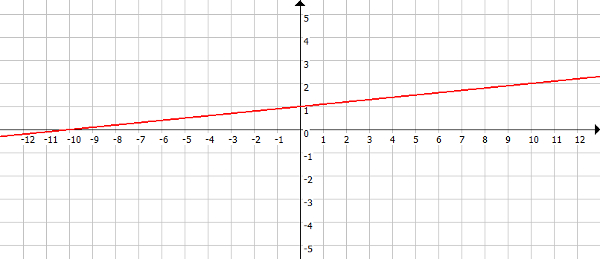
Wo schneidet die Gerade $y=0,1x+1$ die x-Achse?
Um das herauszufinden setzen wir für y eine Null ein und lösen die Gleichung.
$\begin{matrix} y & = & 0,1 x + 1 & |~y=0\\ 0 & = & 0,1 x + 1 & |~~~-1\\ -1 & = & 0,1 x & |~: 0,1\\ -10 & = & x & ~\\ \end{matrix}$
Die x-Achse wird bei -10 geschnitten. Siehe Zeichnung:
 Aufgaben und alte Version
Aufgaben und alte Version
Aufgaben:
Schnittpunkte zweier Geraden berechnen: PDF Dokument
Punktprobe: PDF Dokument
Geradengleichung aus zwei Punkten aufstellen: PDF Dokument
Schnittpunkt mit der x-Achse berechnen: PDF Dokument
Alte Version des Textes: PDF Dokument