Sinussatz

Erweiterung der Trigonometrie

Auch der Sinussatz gilt für alle Dreiecke. Also auch für Dreiecke ohne rechten Winkel.

Wann kommt der Sinussatz zum Einsatz?

Den Sinussatz können wir immer dann verwenden, wenn zwei Winkel und die beiden gegenüberliegenden Seiten eines Dreiecks an der Berechnung beteiligt (als Wert oder als unbekannte Größe) sind. Das Dreieck muss nicht rechtwinklig sein.

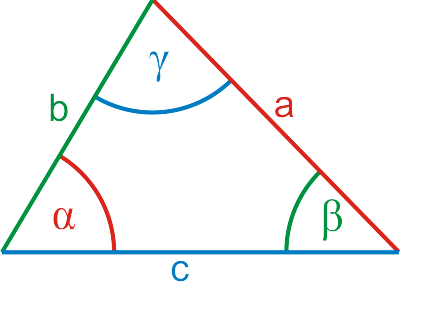
Der Sinussatz gilt ebenfalls nicht nur für rechtwinklige, sondern für alle Dreiecke. Er lautet:

$$\color{red}{\frac{a}{sin(\alpha)}}=\color{green}{\frac{b}{sin(\beta)}}= \color{blue}{\frac{c}{sin(\gamma)}}$$

Tipp 1: Erkennen Sie auch hier das Prinzip, wie Seiten und Winkel im Dreieck und in den Brüchen der Formel gegenüberstehen.

Tipp 2: In den seltensten Fällen benötigen wir alle drei Brüche der Formel und verwenden daher kürzere Formeln mit nur zwei Brüchen:

$$\frac{a}{sin(\alpha)}=\frac{b}{sin(\beta)}\color{#BBBBBB}{=\frac{c}{sin(\gamma)}}$$

oder

$$\frac{a}{sin(\alpha)}\color{#BBBBBB}{=\frac{b}{sin(\beta)}}=\frac{c}{sin(\gamma)}$$

oder

$$\color{#BBBBBB}{\frac{a}{sin(\alpha)}=}\frac{b}{sin(\beta)}=\frac{c}{sin(\gamma)}$$

Um mit dem Sinussatz die Länge einer Seite eines Dreiecks zu berechnen, müssen folgende Größen bekannt sein:

1. Der Winkel, der der gesuchten Seite gegenüberliegt
2. Länge einer anderen Seite und deren gegenüberliegender Winkel

Beispiel:

$$ \begin{array}{} \alpha &=& 20°\\ a &=& 15 cm\\ \gamma &=& 30°\\ c&=&?\\ \end{array} $$

Wir setzen in den Sinussatz ein:

$$ \begin{array}{} \dfrac{15}{sin(20°)}&=&\dfrac{c}{sin(30°)}\\ 43,8571 &=& \dfrac{c}{0,5}~|~\cdot 0,5\\ 21,9 &\approx& c\\ \end{array} $$

Seite c ist etwa 21,9 cm lang.

Vorbemerkung

Im folgenden Diagramm sind die Sinus- und Kosinuswerte eingezeichnet. Auf der waagerechten Achse können wir die Winkel ablesen, auf der senkrechten die Sinus- und Kosinuswerte.

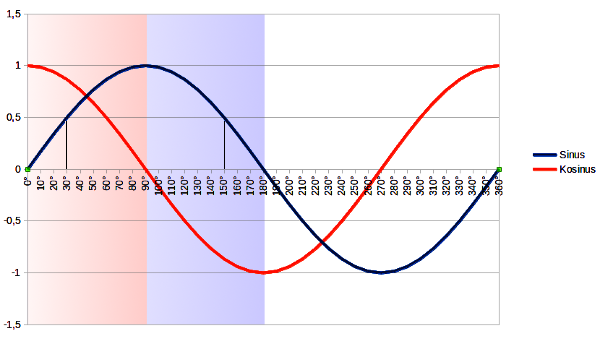
Beide Kurven sind periodisch und schwingen im Prinzip auch für Winkel über 360° weiter. Aber solche Winkel interessieren uns in der Dreiecksberechnung nicht. Für rechtwinklige Dreiecke ist nur der rosa unterlegte Bereich von Interesse. Für allgemeine Dreiecke kommt noch der hellblau unterlegte Bereich dazu.

Welcher Winkel gehört zum Sinuswert 0,5? Der Taschenrechner sagt:

$$ sin^{-1}(0,5) = 30 $$

Aber stimmt das auch?

Wenn wir uns die Sinuskurve genauer anschauen, fällt auf, dass

$$ sin^{-1}(0,5) = 150 $$

auch stimmt. Beide Winkel 30° und 150° kommen in Frage. Der Taschenrechner liefert uns immer nur den kleineren zurück. Den größeren erhalten wir, indem wir den kleineren von 180° abziehen. Beispiel:

$$ 180 - 30 = 150 $$