Kosinussatz

Erweiterung der Trigonometrie

Bisher waren wir bei der Trigonometrie auf rechtwinklige Dreiecke beschränkt. In diesem Block lernen wir den Kosinussatz kennen, der in allen Dreiecken (auch ohne rechten Winkel) gilt.

Wann kommt der Kosinussatz zum Einsatz?

Den Kosinussatz können wir immer dann verwenden, wenn ein Winkel und alle drei Seiten eines Dreiecks an der Berechnung beteiligt (als Wert oder als unbekannte Größe) sind. Das Dreieck muss nicht rechtwinklig sein.

Ausblick

Den Sinussatz, der auch in allen Dreiecken gilt, werden wir dann im nächsten Block behandeln.

Der Kosinussatz lautet:

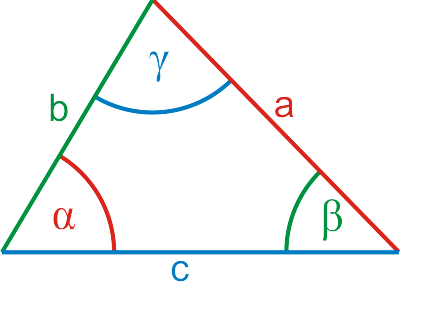
$$\color{red}{a^2}=b^2+c^2-2 \cdot b \cdot c \cdot cos(\color{red}{\alpha})$$ $$\color{green}{b^2}=a^2+c^2-2 \cdot a \cdot c \cdot cos(\color{green}{\beta})$$ $$\color{blue}{c^2}=a^2+b^2-2 \cdot a \cdot b \cdot cos(\color{blue}{\gamma})$$

Tipp: Vergleichen Sie die Farben in der Zeichnung mit den Farben in den Formeln. Erkennen Sie das Prinzip? Entscheidend ist nicht, wie eine Seite oder ein Winkel heißt, sondern welche Seiten den Winkel bilden (in den Formeln schwarz) und welche Seite dem Winkel gegenüber liegt (in den Formeln rot, grün oder blau).

Wenn Sie sich das klar machen, haben Sie keine Schwierigkeiten, wenn die Seiten mal nicht a, b oder c heißen, sondern auf eine andere Weise benannt sind.

Beispiel:

$$ \begin{array}{} a &=& ?\\ b &=& 5 cm\\ c &=& 7 cm\\ \alpha &=& 15°\\ \end{array} $$

Zeichnung (schwarz: gegebene Größen, rot: gesuchte Größe)

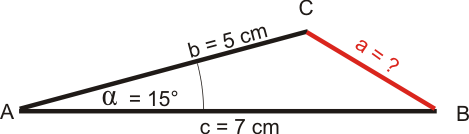
Werte in die Formel einsetzen und ausrechnen:

$a^2 = 5^2+7^2-2 \cdot 5 \cdot 7 \cdot cos(15°)$

$a^2 = 25+49-70 \cdot cos(15°)$

$a^2 = 74-70 \cdot cos(15°)$ Warnung! Siehe unten.

$a^2 = 74-70 \cdot 0,9659$

$a^2 = 74-67,615$

$a^2=6,385 | \sqrt{~}$

$a \approx 2,5$

Erläuterung zur Warnung: Verlockend wäre es an dieser Stelle $74-70=4$ zu rechnen. Machen Sie sich klar, dass das ein Verstoß gegen die Punkt-vor-Strich Regel wäre.

Diesen Irrtum habe ich beim Korrigieren so oft gesehen, dass ich an dieser Stelle ausdrücklich auf diese Fehlerquelle hinweisen möchte.

Beispiel:

$$ \begin{array}{} a &=& 5 cm \\ b &=& 6 cm\\ c &=& 7 cm\\ \alpha &=& ~?\\ \end{array} $$

Zeichnung (schwarz: gegebene Größen, rot: gesuchte Größe)

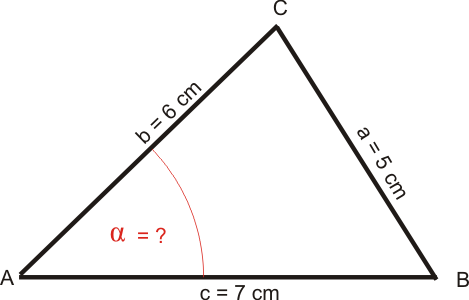
Werte in die Formel einsetzen und ausrechnen:

$$ \begin{array}{rcll} 5^2&=&6^2+7^2-2 \cdot 6 \cdot 7 \cdot cos(\alpha)&~\\ 25&=&36+49-84 \cdot cos(\alpha)&~\\ 25&=&85-84 \cdot cos(\alpha)& | -85\\ -60&=&-84 \cdot cos(\alpha)& | :(-84)\\ 0,7143&=&cos(\alpha)&~\\ cos^{-1}(0,7143)&=&\alpha&~\\ 44° &\approx& \alpha&~\\ \end{array} $$

Beispiel 1:

$$ \begin{array}{} a &=& 4 cm\\ b &=& 6 cm\\ c &=& ~?\\ \alpha = 35°\\ \end{array} $$

Zeichnung (schwarz: gegebene Größen, rot: gesuchte Größe)

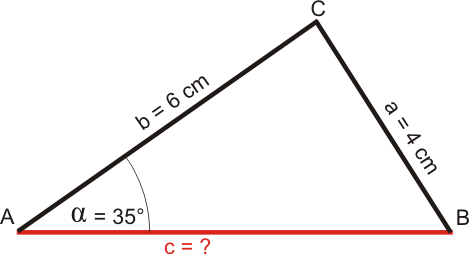
Werte in die Formel einsetzen und ausrechnen:

$$ \begin{array}{rcl} 4^2&=&6^2+c^2-2 \cdot 6 \cdot c \cdot cos(35°)\\ 16&=&36+c^2-9,8298 c\\ 0&=&c^2 - 9,8298 c +20 | pq\\ c_{1;2}&=& - \frac{-9,8298}{2}\pm \sqrt{\left(\frac{-9,8298}{2} \right)^2 -20}\\ c_{1;2}&=& 4,9149 \pm \sqrt{\left(-4,9149\right)^2 -20}\\ c_{1;2}&=& 4,9149 \pm \sqrt{4,1562}\\ c_{1;2}&=&4,9149 \pm 2,0387\\ c_{1} &\approx& 7,0\\ c_{2} &\approx& 2,9\\ \end{array} $$

Wir erhalten (wie so oft bei der Verwendung der pq-Formel) zwei Ergebnisse und beide sind positiv! Aber welches ist denn nun richtig?

Tatsächlich sind beide Ergebnisse richtig, wie die folgende Zeichnung zeigt:

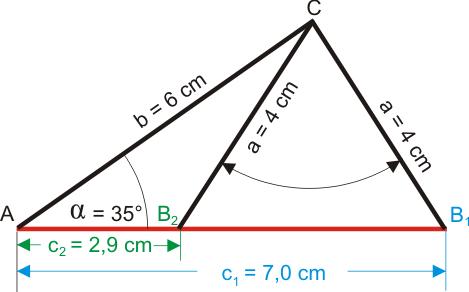
Die Winkel $\beta$ und $\gamma$ wurden in der Aufgabe nicht festgelegt. Wir können die Ecke C daher als Scharnier auffassen, um das wir die Seite a drehen können.

Wir erhalten so zwei Möglichkeiten die 4 cm lange Seite a im Dreieck unterzubringen. Es ist also auch in diesem Fall sinnvoll, dass uns die pq-Formel zwei Resultate liefert!

Beispiel 2:

$$ \begin{array}{} a &=&8 cm\\ b &=& 6 cm\\ c &=& ~?\\ \alpha &=& 60°\\ \end{array} $$

Zeichnung (schwarz: gegebene Größen, rot: gesuchte Größe)

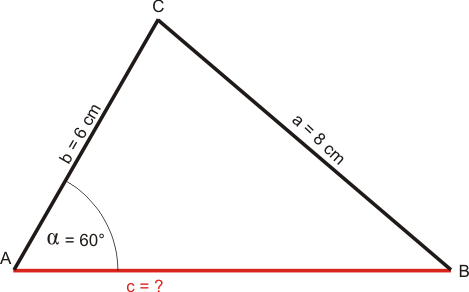
Werte in die Formel einsetzen und ausrechnen:

$$ \begin{array}{rcll} 8^2&=&6^2+c^2-2 \cdot 6 \cdot c \cdot cos(60°)\\ 64&=&36+c^2-6 c\\ 0&=&c^2 - 6 c -36 &| pq\\ c_{1;2}&=& - \frac{-6}{2}\pm \sqrt{\left(\frac{-6}{2} \right)^2 +36}\\ c_{1;2}&=& 3 \pm \sqrt{\left(-3\right)^2 +36}\\ c_{1;2}&=& 3 \pm \sqrt{45}\\ c_{1;2}&=& 3 \pm 6,7082\\ c_{1} &\approx& 9,7\\ c_{2} &\approx& -3,7\\ \end{array} $$

Nun ist auch noch ein Ergebnis negativ! Was soll das schon wieder?

Auch hier sind beide Ergebnisse richtig, wie die folgende Zeichnung zeigt:

Das negative Ergebnis zeigt in die entgegengesetzte (negative) Richtung.

Beispiel 3:

$$ \begin{array}{} a &=& 4 cm\\ b &=& 6 cm\\ c &=&~?\\ \alpha &=& 60°\\ \end{array} $$

Zeichnung (schwarz: gegebene Größen, rot: gesuchte Größe)

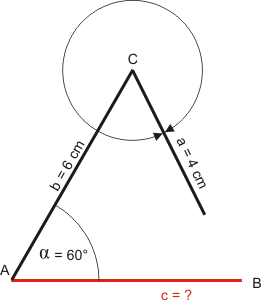
Hier zeigt schon die Zeichnung: Wie auch immer wir Seite a um Ecke C drehen, a ist einfach zu kurz und erreicht Seite c überhaupt nicht. Somit gibt es keine „korrekte Länge“ für c. Mal sehen, wie sich das rechnerisch zeigt:

Setzen wir die Werte in die Formel ein und versuchen die „korrekte Länge“ auszurechnen:

$$ \begin{array}{rcll} 4^2&=&6^2+c^2-2 \cdot 6 \cdot c \cdot cos(60°)\\ 16&=&36+c^2-6 c\\ 0&=&c^2 - 6 c +20 | pq\\ c_{1;2}&=& - \frac{-6}{2}\pm \sqrt{\left(\frac{-6}{2} \right)^2 -20}\\ c_{1;2}&=& 3 \pm \sqrt{\left(-3\right)^2 -20}\\ c_{1;2}&=& 3 \pm \sqrt{-11}\\ \end{array} $$

An dieser Stelle müssen wir die Berechnung abschließen, da es keine reelle Lösung unserer Gleichung gibt.

Wenn es keine „korrekte Länge“ gibt, können wir auch keine ausrechnen!

Nur für Fortgeschrittene

1) Wir teilen das Dreieck mit der Höhe auf c in zwei rechtwinklige Teildreiecke.

2) Das linke Teilstück von c ist die Ankathete zu $\alpha$:

$$ \begin{array}{} cos(\alpha)&=&\displaystyle \frac{c_l}{b}&|\cdot b\\ b\cdot cos(\alpha)&=&c_l\\ \end{array} $$

3) Das rechte Teilstück von c erhalten wir, wenn wir von c das linke Teilstück abziehen:

$$ \begin{array}{} c-b\cdot cos(\alpha)&=&c_r\\ \end{array} $$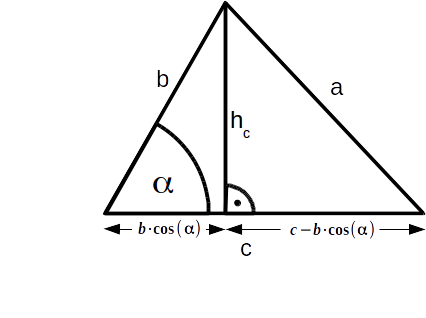

3) Nun stellen wir für beide Teildreiecke den Satz des Pythagoras auf:

$$ \begin{array}{} l:&b^2&=&{h_c}^2+[b \cdot cos(\alpha)]^2\\ r:&a^2&=&{h_c}^2+[c-b\cdot cos(\alpha)]^2\\ l:&b^2&=&{h_c}^2+b^2 \cdot cos^2(\alpha)\\ r:&a^2&=&{h_c}^2+c^2-2 \cdot b \cdot cos(\alpha)+cos^2(\alpha)\cdot b^2\\ \end{array} $$

3) Wir lösen beide Gleichungen nach $h_c$ auf:

$$ \begin{array}{} l:&b^2-b^2 \cdot cos^2(\alpha)&=&{h_c}^2\\ r:&a^2-c^2+2 \cdot b \cdot cos(\alpha)-cos^2(\alpha)\cdot b^2&=&{h_c}^2&\\ \end{array} $$

4) Gleichsetzen und nach $a^2$ auflösen:

$$ \begin{array}{rcl} a^2-c^2+2\cdot b \cdot cos(\alpha) \color{red}{-b^2\cdot cos^2(\alpha)}&=&b^2\color{red}{-b^2 \cdot cos^2(\alpha)}\\ a^2\color{red}{-c^2}+2\cdot b \cdot cos(\alpha)&=&b^2\\ a^2\color{red}{+2\cdot b \cdot cos(\alpha)}&=&b^2+c^2\\ a^2&=&b^2+c^2-2\cdot b \cdot cos(\alpha)\\ \end{array} $$