Start / Rechtwinklige Trigonometrie
Inhalt
Ankathete, Gegenkathete und Hypotenuse
Sinus, Kosinus und Tangens
Fehlerquelle Taschenrechner
Fehlende Größen berechnen
 Ankathete, Gegenkathete und Hypotenuse
Ankathete, Gegenkathete und Hypotenuse
Wie wir bereits vom Satz des Pythagoras wissen, unterscheiden wir in rechtwinkligen Dreiecken:
-
Katheten
(Die zwei Seiten, die miteinander den rechten Winkel bilden.) -
Hypotenuse
(Die andere Seite, die dem rechten Winkel gegenüberliegt.)
Ab jetzt werden wir die beiden Katheten noch einmal unterscheiden, in eine:
-
Ankathete
(Die einen bestimmten Winkel berührt.) -
Gegenkathete
(Die einem bestimmten Winkel gegenüberliegt.)
In der folgenden Zeichnung sind die Seiten a und b Katheten, Seite c ist die Hypotenuse. Der rechte Winkel ist also $\gamma$ (Gamma).
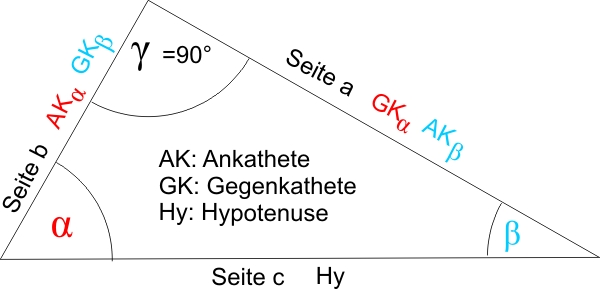
Beachten Sie:
- Seite a ist die Ankathete von $\beta$ und die Gegenkathete von $\alpha$
- Seite b ist die Ankathete von $\alpha$ und die Gegenkathete von $\beta$
Was also Ankathete und Gegenkathete ist, hängt vom Winkel ab, von dem aus wir die Kathete sehen.
 Sinus, Kosinus und Tangens
Sinus, Kosinus und Tangens
Sinus (kurz: sin), Kosinus (kurz: cos) und Tangens (kurz: tan) sind sogenannte Winkelfunktionen. Sie sind wie folgt definiert:
$$ \begin{array}{} sin(\alpha)&=&\displaystyle \frac{GK_\alpha}{Hy}&~~~&sin(\beta)&=&\displaystyle \frac{GK_\beta}{Hy}\\ cos(\alpha)&=&\displaystyle \frac{AK_\alpha}{Hy}&~~~&cos(\beta)&=&\displaystyle \frac{AK_\beta}{Hy}\\ tan(\alpha)&=&\displaystyle \frac{GK_\alpha}{AK_\alpha}&~~~&tan(\beta)&=&\displaystyle \frac{GK_\beta}{AK_\beta}\\ \end{array} $$Zu jedem Winkel existiert ein passender Sinus-, Kosinus- oder Tangenswert. Beispiele:
$$ \begin{array}{} sin(10°)&=&0,17..& &cos(10°)&=&0,98..& &tan(10°)&=&0,17..\\ sin(20°)&=&0,34..& &cos(20°)&=&0,93..& &tan(20°)&=&0,36..\\ sin(30°)&=&0,5& &cos(30°)&=&0,86..& &tan(30°)&=&0,57..\\ sin(40°)&=&0,64..& &cos(40°)&=&0,76..& &tan(40°)&=&0,83..\\ \end{array} $$Die meisten Winkelfunktionswerte sind irrationale Zahlen, also Zahlen mit unendlich vielen Nachkommastellen in unperiodischer Folge. Das hat zur Folge, dass wir im praktischen Rechnen Abstriche bei der Genauigkeit machen müssen.
Um herauszufinden, welcher Winkelfunktionswert zu einem bestimmten Winkel gehört, verwendete man früher Tabellen, heute kommt hier eher ein Taschenrechner zum Einsatz.
Möchten wir zum Beispiel wissen, welcher Kosinuswert zu 35° gehört, rechnen wir:
$$ cos(35) = $$und erhalten $0,819152044$. Das ist die Genauigkeit des Taschenrechners. In Wahrheit sind es unendlich viele Nachkommastellen.
Haben wir dagegen einen Sinuswert von $0,5678$ und möchten den passenden Winkel dazu wissen, rechnen wir:
$$ sin^{-1}(0,5678) = $$und erhalten ungefähr 34,6°.
$sin^{-1}$ ist die Umkehrfunktion, die aus dem Sinuswert wieder einen Winkel macht. Entsprechend gibt es auch $cos^{-1}$ und $tan^{-1}$. Bei den meisten Taschenrechnern erhalten Sie diese Funktion, indem Sie vor der Winkelfunktionstaste die Shift-Taste drücken. Lesen Sie im Zweifel in der Gebrauchsanweisung des Taschenrechners nach.
 Fehlerquelle Taschenrechner
Fehlerquelle Taschenrechner
Achtung! Das funktioniert nur, wenn der Taschenrechner auf die richtige Maßeinheit eingestellt ist. Neben Grad [°] gibt es noch das Bogenmaß [rad], Gon [gon] und andere. Beispielumrechnung:
$$ 90° = 1,5708~rad = 100~gon $$Bei unbedachtem Herumtippen auf der Tastatur des Taschenrechners kann er unbemerkt auf eine andere Maßeinheit umgestellt werden. Wenn Sie von einer anderen Maßeinheit ausgehen als der Taschenrechner, erhalten Sie falsche Zahlen!
Für den Realschulunterricht sollte der Taschenrechner auf Grad (englisch Degree, kurz: deg oder d) eingestellt sein. Die meisten Taschenrechner zeigen in ihrem Display an auf welche Winkelmaßeinheit sie eingestellt sind. Lesen Sie im Zweifel in der Gebrauchsanweisung nach.
 Fehlende Größen berechnen
Fehlende Größen berechnen
Das Berechnen einer fehlenden Größe in einem rechtwinkligen Dreieck mit Hilfe der Winkelfunktionen geschieht in drei Schritten:
- Passende Winkelfunktionsformel wählen
- Bekannte und unbekannte Größen in die Formel einsetzen
- Gleichung lösen
Beispiel 1:
$$ \begin{array}{} \alpha&=&30°\\ Hy&=&10~cm\\ GK&=& ?\\ \end{array} $$Passende Winkelfunktionsformel wählen
$$ \begin{array}{} sin(\alpha)&=&\displaystyle \frac{GK}{Hy}\\ cos(\alpha)&=&\displaystyle \frac{AK}{Hy}\\ tan(\alpha)&=&\displaystyle \frac{GK}{AK}\\ \end{array} $$Wir entscheiden uns für Sinus, weil nur hier Winkel, Hypotenuse und Gegenkathete vorkommen.
Bekannte und unbekannte Größen in die Formel einsetzen
$$ \begin{array}{} sin(30)&=&\displaystyle \frac{x}{10}\\ \end{array} $$Gleichung lösen
$$ \begin{array}{rcll} sin(30)&=&\displaystyle \frac{x}{10}&| \cdot 10\\ sin(30) \cdot 10&=&x&~\\ 5&=&x&~\\ \end{array} $$Die Gegenkathete ist 5 cm lang.
Beispiel 2:
$$ \begin{array}{} GK&=&5~cm\\ AK&=&8~cm\\ \alpha&=& ?\\ \end{array} $$Passende Winkelfunktionsformel wählen
$$ \begin{array}{} sin(\alpha)&=&\displaystyle \frac{GK}{Hy}\\ cos(\alpha)&=&\displaystyle \frac{AK}{Hy}\\ tan(\alpha)&=&\displaystyle \frac{GK}{AK}\\ \end{array} $$Wir entscheiden uns für Tangens, weil nur hier Winkel, Gegenkathete und Ankathete vorkommen.
Bekannte und unbekannte Größen in die Formel einsetzen
$$ \begin{array}{} tan(x)&=&\displaystyle \frac{5}{8}\\ \end{array} $$Gleichung lösen
$$ \begin{array}{rcll} tan(x)&=&\displaystyle \frac{5}{8}\\ tan(x)&=&0,625\\ x&=&tan^{-1}(0,625)\\ x&\approx&32\\ \end{array} $$Der Winkel beträgt 32°.