Quadratische Funktionen, Parabeln

Quadratische Funktionen

Quadratische Funktionen sind Funktionen des Typs: $y=ax^2+bx+c$

Wobei in einer konkreten Funktion für $a, b, c$ Zahlen stehen. Beispiel: $y=2x^2-3x+1$

Parabeln

Parabeln sind die Graphen quadratischer Funktionen im Koordinatensystem. Beispiel: Die Funktion $y=2x^2-3x+1$ hat den Graphen:

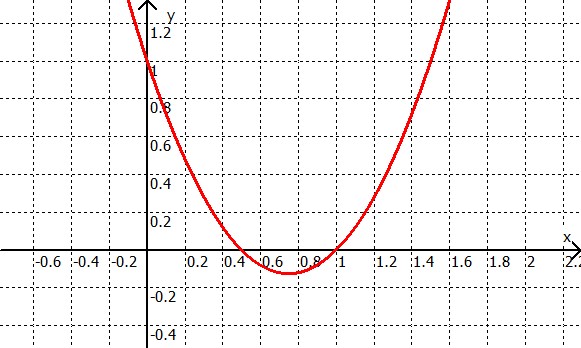
Wir sehen, dass Parabeln keine Geraden, sondern gebogen sind. Um sie einigermaßen sauber zu zeichnen, müssen wir bei Parabeln deutlich mehr als zwei Punkte berechnen.

Schnittpunkt mit der y-Achse

Jede Parabel hat genau einen Schnittpunkt mit der y-Achse. In unserem Beispiel oben schneidet die Parabel die y-Achse bei 1.

Schnittpunkte mit der x-Achse

Beispiele:

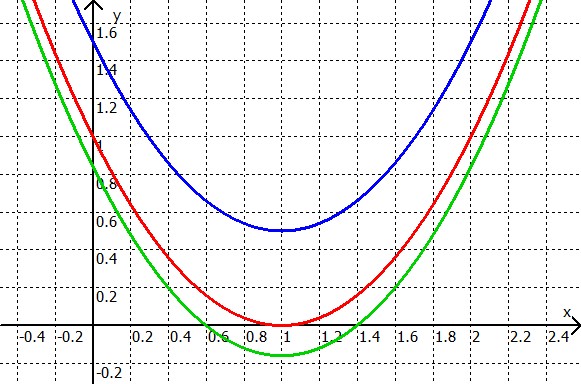
Die Beispiele zeigen: Eine Parabel kann die x-Achse einmal (rot), zweimal (grün) oder auch gar nicht (blau) schneiden.

Scheitelpunkt

Beispiele:

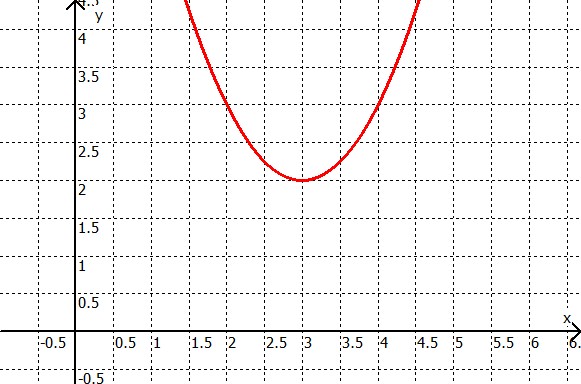
Jede Parabel hat einen sogenannten Scheitelpunkt. Das ist die Stelle, an der die Parabel am stärksten gebogen ist.

Im obigen Beispiel liegt der Scheitelpunkt bei (3|2).

Wie eine Parabel gebogen ist, können wir unmittelbar aus der Gleichung ablesen, ohne dafür rechnen zu müssen.

Beispiele:

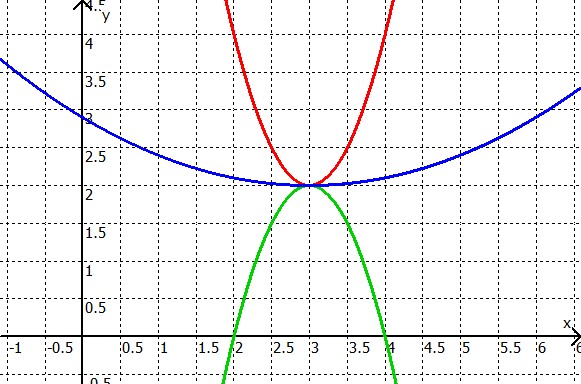
Die rote und die blaue Parabel sind nach oben gekrümmt, die grüne dagegen nach unten.

Die rote und die grüne Parabel sind stark gekrümmt, die blaue dagegen sanft.

Krümmungsregeln:

Legen wir die allgemeine Parabelgleichung $y=ax^2+bx+c$ zugrunde, so gilt:

• $a > 0$   Krümmung nach oben.
• $a < 0$    Krümmung nach unten.
• $|a| > 1$    Starke Krümmung.
• $|a| < 1$    Sanfte Krümmung.
• $|a| = 1$    "Normale" Krümmung.

Gleichungen unseres obigen Beispiels:

Rote Parabel:

$y=2x^2-12x+20$      $2>0$ und $|2|>1$   starke Krümmung nach oben.

Blaue Parabel:

$0,1x^2-0,6x +2,9$       $0,1>0$ und $|0,1|<1$  sanfte Krümmung nach oben.

Grüne Parabel:

$y=-2x^2+12x-16$      $-2<0$ und $|-2|>1$   starke Krümmung nach unten.

Um den Schnittpunkt mit der y-Achse zu berechnen, setzen wir für x eine Null ein und rechnen das entsprechende y aus.

Das funktioniert immer, da jede Parabel die y-Achse genau einmal schneidet.

Beispiel:

Wo schneidet die Parabel zur Funktionsgleichung $y=0,5x^2+2x+3$ die y-Achse?

$\begin{array}{rcll} y&=&0,5x^2+2x+3&|~x=0\\ y&=&0,5 \cdot 0^2+2 \cdot 0+3\\ y&=&3\\ \end{array}$

Die y-Achse wird bei 3 geschnitten.

Bezogen auf die allgemeine Gleichung $y=ax^2+bx+c$ zeigt uns immer der Wert $c$ wo die y-Achse geschnitten wird.

Um die Schnittpunkte mit der x-Achse zu berechnen, setzen wir für y eine Null ein und rechnen, falls möglich, x aus.

Das führt zu einer Gleichung, die mit der pq-Formel bearbeitet werden kann.

Ist die Gleichung nicht lösbar, gibt es auch keine Schnittpunkte der Parabel mit der x-Achse.

Anmerkung: Die Schnittpunkte mit der x-Achse heißen auch Nullstellen.

Beispiele:

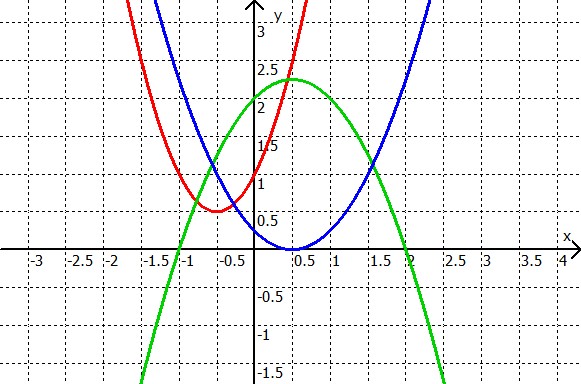
Die Zeichnung zeigt uns:

• Die rote Parabel schneidet die x-Achse überhaupt nicht.
• Die blaue Parabel berührt die x-Achse einmal bei 0,5.
• Die grüne Parabel schneidet die x-Achse zweimal bei -1 und 2.

Wenn uns keine Zeichnung zur Verfügung steht, berechnen wir die Schnittpunkte wie oben beschrieben.

Rote Parabel:

Die Gleichung lautet: $y=2x^2+2x+1$.

$\begin{array}{rcll} y&=&2x^2+2x+1&|y=0\\ 0&=&2x^2+2x+1&|:2\\ 0&=&x^2+1x+0,5&|pq\\ x_{1;2}&=&- \frac{1}{2} \pm \sqrt{\left( \frac{1}{2}\right)^2-0,5}\\ x_{1;2}&=&- 0,5 \pm \sqrt{\left( 0,5\right)^2-0,5}\\ x_{1;2}&=&- 0,5 \pm \sqrt{0,25-0,5}\\ x_{1;2}&=&- 0,5 \pm \sqrt{-0,25}\\ \end{array}$

Keine reelle Lösung, die rote Parabel hat also auch rechnerisch keine Schnittpunkte mit der x-Achse.

Blaue Parabel:

Die Gleichung lautet: $y=x^2-x+0,25$.

$\begin{array}{rcll} y&=&x^2-x+0,25&|~y=0\\ 0&=&x^2-x+0,25&|~pq\\ x_{1;2}&=&- \frac{-1}{2} \pm \sqrt{\left( \frac{-1}{2}\right)^2-0,25}\\ x_{1;2}&=&0,5 \pm \sqrt{\left( -0,5\right)^2-0,25}\\ x_{1;2}&=&0,5 \pm \sqrt{0,25-0,25}\\ x_{1;2}&=&0,5 \pm \sqrt{0}\\ x_{1;2}&=&0,5 \pm 0\\ x_{1;2}&=&0,5\\ \end{array}$

Eine Lösung, die blaue Parabel hat einen Schnittpunkt mit der x-Achse bei 0,5.

Grüne Parabel:

Die Gleichung lautet: $y=-x^2+x+2$.

$\begin{array}{rcll} y&=&-x^2+x+2&|y=0\\ 0&=&-x^2+x+2&|:(-1)\\ 0&=&x^2-x-2&|pq\\ x_{1;2}&=&- \frac{-1}{2} \pm \sqrt{\left( \frac{-1}{2}\right)^2-(-2)}\\ x_{1;2}&=&0,5 \pm \sqrt{\left(-0,5\right)^2+2}\\ x_{1;2}&=&0,5 \pm \sqrt{0,25+2}\\ x_{1;2}&=&0,5 \pm \sqrt{2,25}\\ x_{1;2}&=&0,5 \pm 1,5\\ x_{1}&=&0,5 + 1,5\\ x_{1}&=&2\\ x_{2}&=&0,5 - 1,5\\ x_{2}&=&-1\\ \end{array}$

Zwei Lösungen, die grüne Parabel hat zwei Schnittpunkte mit der x-Achse bei -1 und 2.

Beachten Sie, dass unsere Berechnungen mit der Zeichnung übereinstimmen.

Um den Scheitelpunkt zu berechnen, formen wir die Parabelgleichung von der Normalform:

$$y=ax^2+bx+c$$

in die Scheitelpunktform:

$$y=a(x-x_s)^2+y_s$$

um. Der Scheitelpunkt liegt dann bei $(x_s|y_s)$.

Achtung: Bei der x-Koordinaten wird das Vorzeichen gedreht, bei der y-Koordinaten dagegen nicht!

Beispiel:

Wo ist der Scheitelpunkt der Parabel mit der Funktionsgleichung $y=2x^2-16x+35$?

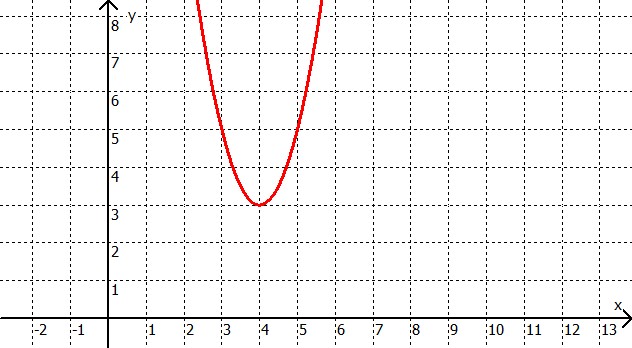
Die Zeichnung sagt uns, dass der Scheitelpunkt bei (4|3) liegt.

Wir formen um:

$$y=2x^2-16x+35$$

Wir klammern aus den Elementen, die $x$ enthalten, den Faktor vor $x^2$ aus:

$$y=2[x^2-8x]+35$$

Nun addieren wir in der Klammer das Quadrat der Hälfte des Faktors vor $x$ (Quadratische Ergänzung: $\left(\frac{-8}{2}\right)^2=16$) und damit dabei kein Fehler entsteht (wir dürfen ja nicht auf einer Gleichungsseite etwas addieren und auf der anderen nicht), ziehen wir den Wert direkt wieder ab:

$$y=2[x^2-8x+16-16]+35$$

Jetzt bilden die ersten drei Elemente in der Klammer einen binomischen Ausdruck, den wir entsprechend umformen:

$$y=2[(x-4)^2-16]+35$$

Wir lösen die eckige Klammer auf:

$$y=2(x-4)^2-32+35$$

Vereinfachen:

$$y=2(x-4)^2+3$$

Jetzt können wir die Koordinaten des Scheitelpunktes ablesen: (4|3). Nicht vergessen: Bei der x-Koordinaten wird das Vorzeichen gedreht, bei der y-Koordinaten dagegen nicht!

Wir können eine Gleichung auch von der Scheitelpunktform in die Normalform umwandeln, wie sich am obigen Beispiel zeigen läßt:

$$y=2(x-4)^2+3$$

Binomische Formel anwenden:

$$y=2(x^2-8x+16)+3$$

Klammer auflösen (Distributivgesetz):

$$y=2x^2-16x+32+3$$

Zusammenfassen:

$$y=2x^2-16x+35$$

Um zu prüfen, ob ein Punkt auf einer Parabel liegt, setzen wir seine Koordinaten in die Funktionsgleichung der Parabel ein.

Beispiel:

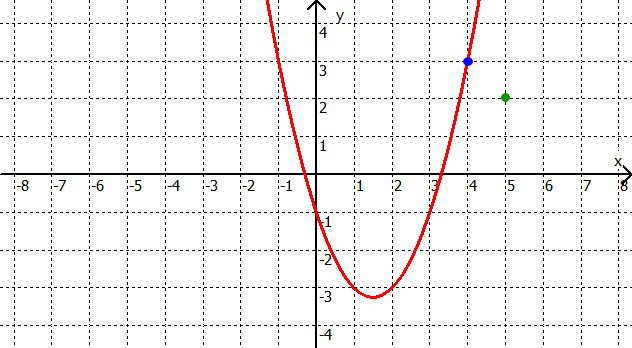
Die Zeichnung zeigt uns, dass der blaue Punkt auf der Parabel liegt, der grüne Punkt dagegen nicht.

Rechnerische Prüfung des blauen Punktes:

$\begin{array}{rcll} y&=&~x^2-3x-1~~~~~~|~x=4~~y=3\\ 3&=^?&4^2-3\cdot 4-1\\ 3&=^?&16-12-1\\ 3&=&3\\ \end{array}$

Der Punkt liegt auf der Parabel.

Rechnerische Prüfung des grünen Punktes:

$\begin{array}{rcll} y&=&~x^2-3x-1&|~x=5~~y=2\\ 2&=^?&5^2-3\cdot 5-1\\ 2&=^?&25-15-1\\ 2 &\not=& 9\\ \end{array}$

Der Punkt liegt nicht auf der Parabel.

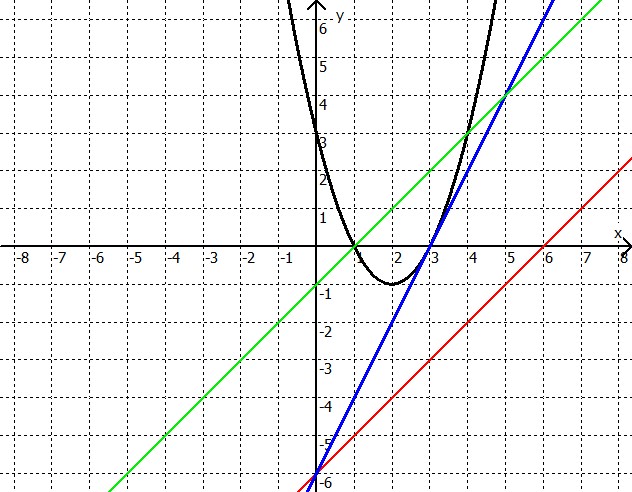
Die Grafik zeigt eine Parabel (schwarz) und drei Geraden (rot, grün und blau).

• Die rote Gerade läuft an der Parabel vorbei: Es gibt gibt keinen Schnittpunkt.
• Die blaue Gerade berührt die Parabel knapp: Es gibt gibt einen Schnittpunkt.
• Die grüne Gerade schneidet die Parabel zwei mal: Es gibt zwei Schnittpunkte.

Zum Berechnen der Schnittpunkte setzen wir die Gleichungen der Parabel und der Geraden gleich.

Beispiel grüne Gerade:

Gerade: $y = x-1$

Parabel: $y = x^2-4x+3$

$ \begin{array}{rrcrrrcr} x&-1&=&x^2&-4x&+3&|&-x\\ ~&-1&=&x^2&-5x&+3&|&+1\\ ~&0&=&x^2&-5x&+4&|&pq\\ \end{array} $

 

$ \begin{array}{rcl} x_{1;2} & = & - \frac{-5}{2}\pm \sqrt {\left( \frac{-5}{2} \right )^2 - (4)}\\ x_{1;2} & = &2,5\pm \sqrt {6,25-4}\\ x_{1;2} & = &2,5\pm \sqrt {2,25}\\ x_{1;2} & = &2,5\pm 1,5\\ x_{1} & = &4\\ x_{2} & =&1\\ \end{array} $

Nun kennen wir die x-Koordinaten und berechnen die y-Koordinaten, indem wir den Wert für x in eine der beiden Gleichungen einsetzen. Wir entscheiden uns für die Geradengleichung. Die Parabelgleichung würde zum gleichen Ergebnis führen, allerdings wäre der Rechenaufwand beträchtlich höher.

$ \begin{array}{rcr} y&=&4 -1\\ y&=&3\\ ~&~&~\\ y&=&1 -1\\ y&=&0\ \end{array} $

Wir erhalten somit die Schnittpunkte (4|3) und (1|0), was mit der Zeichnung übereinstimmt.

Beispiel blaue Gerade:

Gerade: $y = 2x-6$

Parabel: $y = x^2-4x+3$

$ \begin{array}{rrcrrrcr} 2x&-6&=&x^2&-4x&+3&|&-2x\\ ~&-6&=&x^2&-6x&+3&|&+6\\ ~&0&=&x^2&-6x&+9&|&pq\\ \end{array} $

 

$ \begin{array}{rcl} x_{1;2} & = & - \frac{-6}{2}\pm \sqrt {\left( \frac{-6}{2} \right )^2 - (9)}\\ x_{1;2} & = &3\pm \sqrt {9-9}\\ x_{1;2} & = &3\pm \sqrt {0}\\ x_{1;2} & = &3\pm 0\\ x_{1} & = &3\\ x_{2} & =&3\\ \end{array} $

Nun noch die y-Koordinate berechnen:

$ \begin{array}{rcr} y&=&2 \cdot 3 -6\\ y&=&0\\ \end{array} $

Wir erhalten somit einen Schnittpunkt (3|0), auch das entspricht der Zeichnung.

Beispiel rote Gerade:

Gerade: $y = x-6$

Parabel: $y = x^2-4x+3$

$ \begin{array}{rrcrrrcr} x&-6&=&x^2&-4x&+3&|&-x\\ ~&-6&=&x^2&-5x&+3&|&+6\\ ~&0&=&x^2&-5x&+9&|&pq\\ \end{array} $

 

$ \begin{array}{rcl} x^2-5x+9&=& 0\\ x_{1;2} & = & - \frac{-5}{2}\pm \sqrt {\left( \frac{-5}{2} \right )^2 - (9)}\\ x_{1;2} & = &2,5\pm \sqrt {6,25-9}\\ x_{1;2} & = &2,5\pm \sqrt {-2,75}\\ x_{1;2} & = &2,5\pm \text{ k.r.L.} \\ x_{1} & = & \text{ k.r.L.}\\ x_{2} & = & \text{ k.r.L.}\\ \end{array} $

Die Berechnung der y-Koordinaten erübrigt sich. Es gibt keine Schnittpunkte. Auch das deckt sich mit der Zeichnung.

Wie bei Geraden und Parabeln, können zwei Parabeln:

• zwei Schnittpunkte haben
• genau einen Schnittpunkt haben
• ohne Schnittpunkt aneinander vorbeilaufen

Die Berechnung erfolgt wie bei Gerade und Parabel durch Gleichsetzung.

Beispiel: Zwei Schnittpunkte

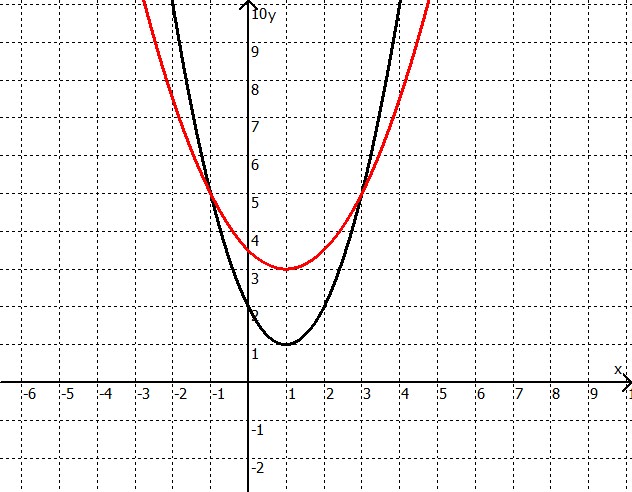
Schwarze Parabel: $y = x^2-2x+2$

Rote Parabel: $y = 0,5x^2-x+3,5$

Gleichsetzen:

$ \begin{array}{rrrcrrrcr} x^2&-2x&+2&=&0,5x^2&-x&+3,5&|&-x^2\\ ~&-2x&+2&=&-0,5x^2&-x&+3,5&|&+2x\\ ~&~&+2&=&-0,5x^2&+x&+3,5&|&-2\\ ~&~&0&=&-0,5x^2&+x&+1,5&|&:(-0,5)\\ ~&~&0&=&x^2&-2x&-3&|&pq\\ \end{array} $

 

$ \begin{array}{rcl} x_{1;2} & = & - \frac{-2}{2}\pm \sqrt {\left( \frac{-2}{2} \right )^2 - (-3)}\\ x_{1;2} & = &1\pm \sqrt {1+3}\\ x_{1;2} & = &1\pm \sqrt {4}\\ x_{1;2} & = &1\pm 2\\ x_{1} & = &3\\ x_{2} & =&-1\\ \end{array} $

Berechnung der y-Koordinaten:

$ \begin{array}{rcr} y&=&(-1)^2-2 \cdot (-1)+2\\ y&=&1+2+2\\ y&=&5\\ ~&~&~\\ y&=&3^2-2 \cdot 3+2\\ y&=&9-6+2\\ y&=&5\\ \end{array} $

Wir haben zwei Schnittpunkte berechnet (-1|5) und (3|5) (Vergl. Zeichnung).

Beispiel: Ein Schnittpunkt

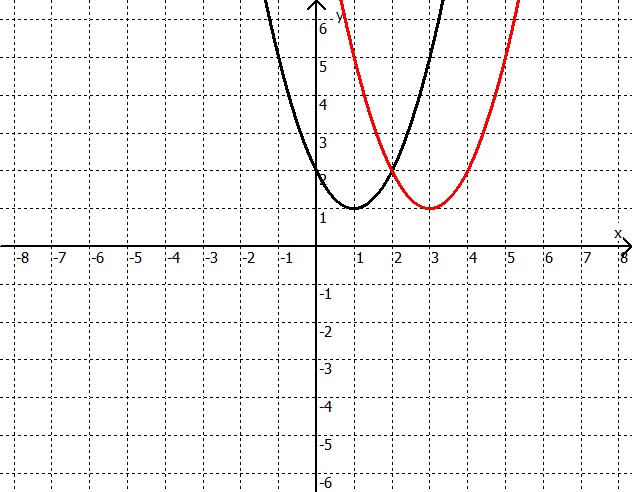
Schwarze Parabel: $y = x^2-2x+2$

Rote Parabel: $y = x^2-6x+10$

Gleichsetzen:

$ \begin{array}{rrrcrrrcr} x^2&-2x&+2&=&x^2&-6x&+10&|&-x^2\\ ~&-2x&+2&=&~&-6x&+10&|&+6x\\ ~&4x&+2&=&~&~&10&|&-2\\ ~&4x&~&=&~&~&8&|&:4\\ ~&x&~&=&~&~&2&~&~\\ \end{array} $

Einsetzen in eine der Gleichungen, um die y-Koordinate zu berechnen:

$\begin{array}{rcl} y &=& 2^2-2 \cdot 2+2\\ y &=& 4-4+2\\ y &=& 2\\ \end{array}$

Der Schnittpunkt liegt bei (2|2) (vergl. Zeichnung).

Anmerkung: Im obigen Beispiel lief die Berechnung nicht auf eine pq-Formel hinaus. Das kann, muss aber nicht sein. Im Falle, dass die Berechnung eine pq-Formel enthalten hätte, könnten wir auch zwei x-Werte (d.h. zwei Schnittpunkte) oder keine reelle Lösung (d.h. keine Schnittpunkte) erhalten können.

Beispiel: Kein Schnittpunkt

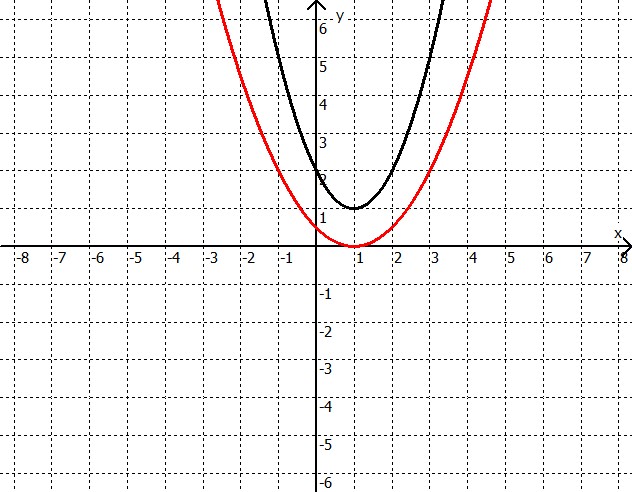
Schwarze Parabel: $y = x^2-2x+2$

Rote Parabel: $y = 0,5x^2-x+0,5$

Gleichsetzen:

$ \begin{array}{rrrcrrrcr} x^2&-2x&+2&=&0,5x^2&-x&+0,5&|&-x^2\\ ~&-2x&+2&=&-0,5x^2&-x&+0,5&|&+2x\\ ~&~x&+2&=&-0,5x^2&+x&+0,5&|&-2\\ ~&~x&0&=&-0,5x^2&+x&-1,5&|&:0,5\\ ~&~x&0&=&x^2&-2x&+3&|&pq\\ \end{array} $

 

$ \begin{array}{rcl} x_{1;2} & = & - \frac{-2}{2}\pm \sqrt {\left( \frac{-2}{2} \right )^2 - (3)}\\ x_{1;2} & = &1\pm \sqrt {1-3}\\ x_{1;2} & = &1\pm \sqrt {-2}\\ x_{1;2} & = &1\pm \text{ k. r. L} \\ x_{1} & = & \text{ k. r. L}\\ x_{2} & = & \text{ k. r. L}\\ \end{array} $

Da es keine Schnittpunkte (k. r. L.: keine reelle Lösung) gibt (vergl. Zeichnung), brauchen wir keine y-Koordinaten zu berechnen.

N ∪ ↑ ∪ ↓ ∪ → ∪ ← ∪ → ∪ ← → ∩ ← Löschen $\small y=ax^2+bx+c$ $a:$  $b:$  $c:$  mit diesen Werten

Funktionsgleichung:                   

Erläuterungen zu dieser Animation

Zweck dieser Animation ist es, auf spielerische Weise ein Gespür dafür zu bekommen, wie Lage und Krümmung einer Parabel mit ihrer Gleichung zusammenhängen.

Wenn sich die Maus über einem Button, einem Eingabefeld, einer Formel usw. befindet zeigt sich ein Tooltip, der genauere Hinweise gibt, welche Aufgabe dieses Element hat.

Sie können durch den Button „N ∪“ eine Normalparabel zeichnen. Der Button „mit diesen Werten“ zeichnet eine Parabel mit den in die Eingabefelder geschriebenen Werten a, b, c für die Gleichung in Normalform.

Die zuletzt gezeichnete Parabel kann mit den entsprechenden Buttons nach oben, unten, rechts und links verschoben, beziehungsweise nach oben oder unten gebogen werden. Beachten Sie, wie sich dabei die Gleichungen verändern.

Ist „Löschen“ gewählt, wird die alte Parabel gelöscht, sodass Sie nur die neue Parabel sehen können. Ist „Löschen“ nicht gewählt, sehen Sie auch noch die alten Parabeln. Beim Verschieben entsteht so eine Spur. Bei zwei Parabeln können Sie, falls vorhanden, die Schnittpunkte sehen.

Mit den drei Schiebereglern kann die Farbe des Graphen verändert werden. Der obere Regler stellt den Rotanteil ein, der mittlere den Grünanteil und der untere den Blauanteil. Steht der Schieber ganz links, ist der entsprechende Anteil ganz dunkel. Steht der Schieber ganz rechts, hat der entsprechende Farbanteil die volle Leuchtkraft. Die geänderte Farbe macht sich dann bei der nächsten Neuzeichnung der Parabel bemerkbar.

Werden die Buttons zum Verschieben oder Verbiegen der Parabel in zu rascher Folge (>Doppelklickgeschwindikeit) geklickt, können sich die Gleichungen verheddern, wodurch sie unleserlich werden. In diesem Falle etwas langsamer weiterklicken und die Formeln sind wieder ordentlich.

Scheitelpunkte und Schnittpunkte mit den Koordinatenachsen
Punktprobe
Alte PDF Version