Länge, Fläche, Volumen

Einen Weg können wir gehen oder fahren. Kurze Wege auf einem Blatt Papier können wir mit dem Finger nachfahren. Mit Länge bezeichnen wir, wie weit ein Weg ist.

Eine Länge ist eine eindimensionale Größe.

Typische Längen

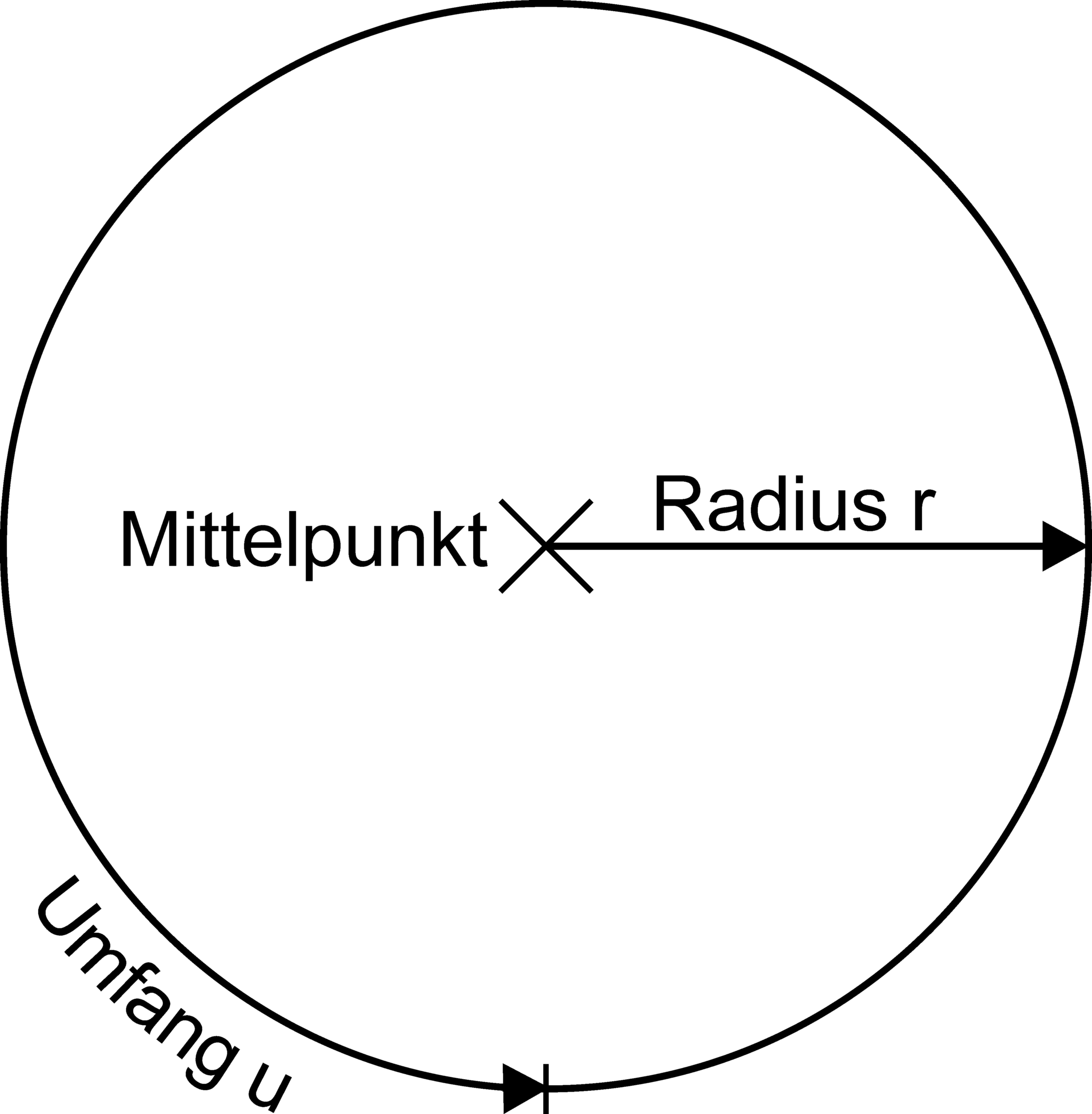
Umfang und Radius eines Kreises.

Typische Messgeräte

Kilometerzähler des Autos
Lineale
Messbänder
u.s.w.

Maßeinheiten

Millimeter	Zentimeter	Dezimeter	Meter
1 mm	0,1 cm	0,01 dm	0,001 m
10 mm	1 cm	0,1 dm	0,01 m
100 mm	10 cm	1 dm	0,1 m
1 000 mm	100 cm	10 dm	1 m

 

Meter	Kilometer
1 m	0,001 km
1 000 m	1 km

Eine Fläche ist etwas, das wir beispielsweise mit Farbe ausmalen könnten.

Eine Fläche ist eine zweidimensionale Größe.

Typische Fläche

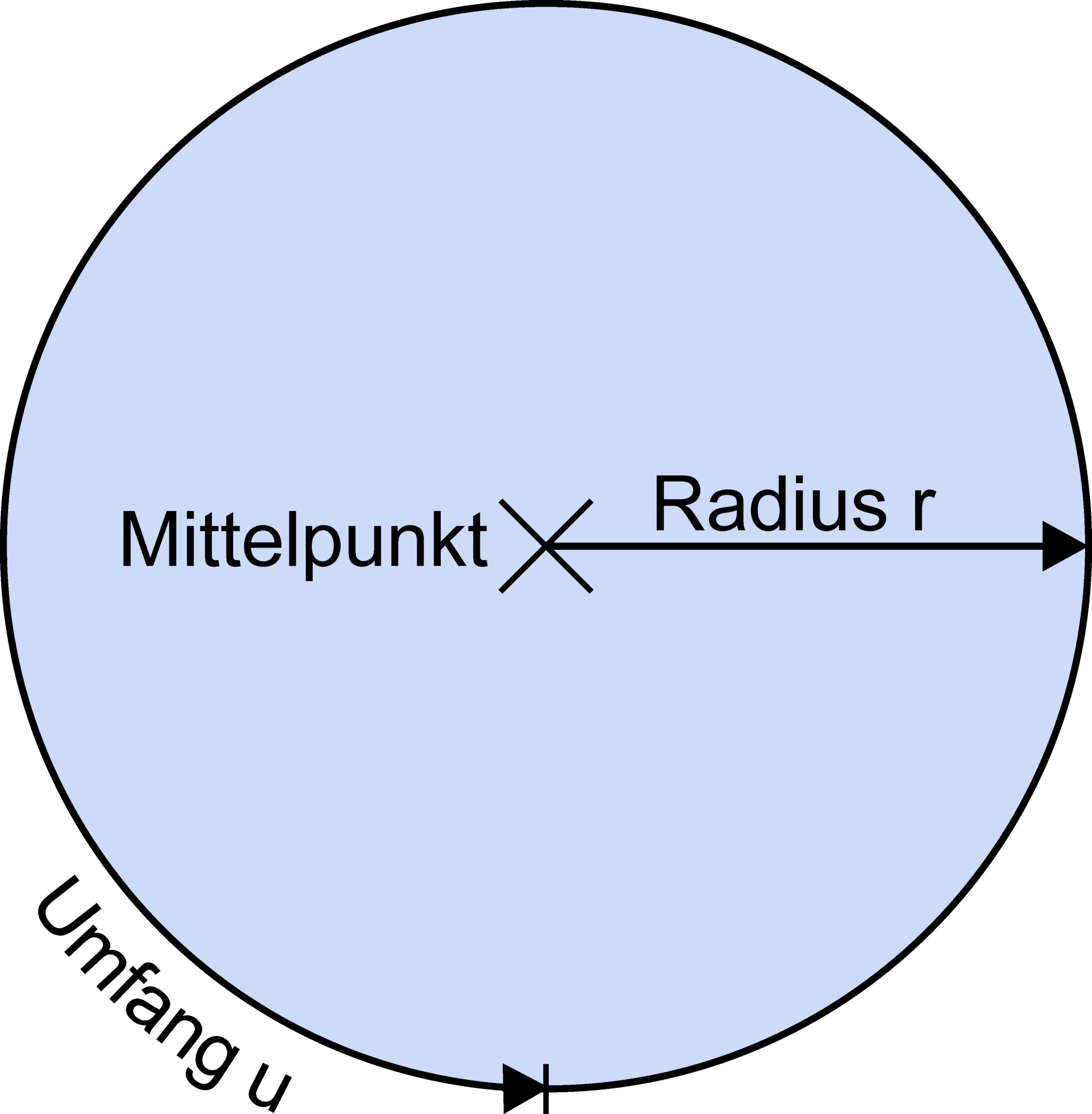
Der blau eingefärbte Bereich des Kreises ist seine Fläche.

Anmerkung: Umfang und Radius sind und bleiben natürlich Längen!

Typische Messgeräte

Flächen werden in der Praxis eher berechnet, als gemessen

Maßeinheiten

Quadratmillimeter	Quadratzentimeter	Quadratdezimeter	Quadratmeter
1 mm²	0,01 cm²	0,0001 dm²	0,000001 m²
100 mm²	1 cm²	0,01 dm²	0,0001 m²
10 000 mm²	100 cm²	1 dm²	0,01 m²
1 000 000 mm²	10 000 cm²	100 dm²	1 m²

 

Quadratmeter	Quadratkilometer
1 m²	0,000001 km²
1 000 000 m²	1 km²

Ein Volumen ist ein Raum, den wir, sofern er noch leer ist, mit irgendeinem Material füllen könnten.

Ein Volumen ist eine dreidimensionale Größe.

Typisches Volumen

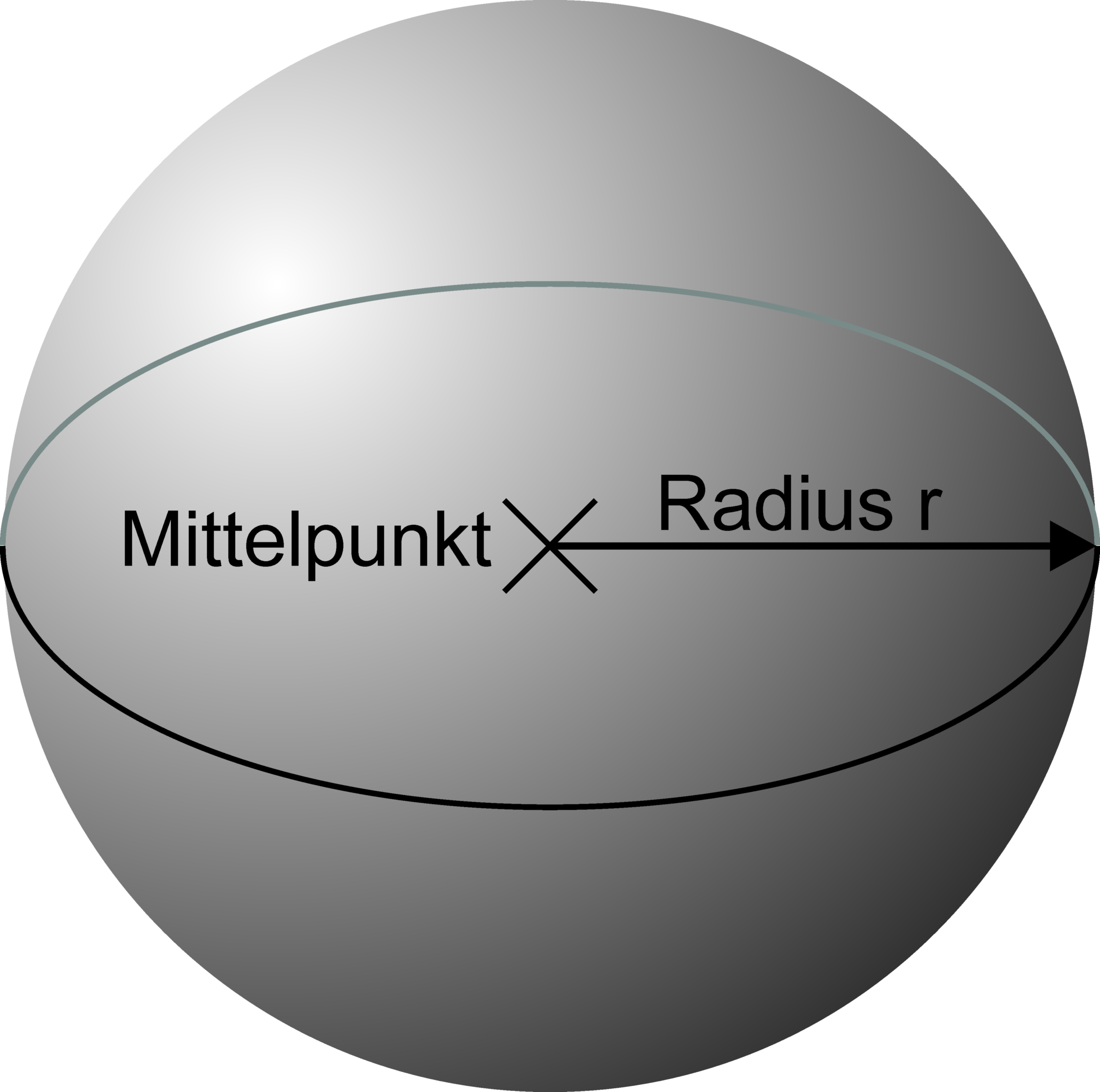
Der Raum, den die Kugel einnimmt, ist ihr Volumen.

Anmerkung: Eine Kugel hat auch eine Oberfläche, die wir mit Farbe anmalen könnten. Sie hat auch Längen: Den Radius und den Umfang.

Typische Messgeräte

Wenn das Volumen leer ist, könnten wir mit einem Messbecher feststellen, wieviel Flüssigkeit wir hineingießen können.

Maßeinheiten

Kubikmillimeter	Kubikzentimeter	Kubikdezimeter	Kubikmeter
1 mm³	0,001 cm³	0,000001 dm³	0,000000001 m³
1000 mm³	1 cm³	0,001 dm³	0,000001 m³
1 000 000 mm³	1000 cm³	1 dm³	0,001 m³
1 000 000 000 mm³	1 000 000 cm³	1 000 dm³	1 m³

 

Kubikmeter	Kubikkilometer
1 m³	0,000000001 km³
1 000 000 000 m³	1 km³

Längen

Zentimeter	Zoll (engl. inch)
1 cm	0,39 '' (in)
2,54 cm	1 '' (in)

Flächen

Quadratmeter	Ar
1 m²	0,01 a
100 m²	1 a

Ar	Hektar
1 a	0,01 ha
100 a	1 ha

Volumen

Kubikzentimeter	Liter
1 cm³	0,001 ℓ
1000 cm³	1 ℓ

Am ersten Unterrichtstag wurde Ihnen eine Formelsammlung ausgehändigt, auf der sich eine ganze Reihe von Formeln zur Berechnung verschiedener Umfänge, Flächen und Volumen finden.

Beispiel: Kreisumfang

Die Formel zur Berechnung des Umfangs eines Kreises lautet: $U=2 \cdot \pi \cdot r$. Sprich: „U gleich zwei mal Pi mal r “

Mit Pi ist die sogenannte Kreiszahl $3,14159265...$ gemeint. Sie müssen diese Zahl auf dem Taschenrechner nicht von Hand eingeben. Dafür gibt es eine Pi-Taste. Der Buchstabe r bezeichnet den Radius (Abstand des Mittelpunktes vom Kreisrand).

Bei einer Prüfungsaufgabe müssten Sie spätestens im Antwortsatz die Maßeinheit des Ergebnisses angeben. Der Umfang ist eine Länge. Wurde der Radius in cm angegeben, liefert die Formel das Ergebnis ebenfalls in cm.

Gelegentlich wird in der Aufgabe verlangt das Ergebnis in einer anderen Maßeinheit anzugeben. In diesem Fall müssten Sie den Wert umrechnen (siehe oben).

Beispiel: Fläche eines Rechtecks

Die Formel lautet: $A=a \cdot b$.

Sind a und b in der Aufgabe in $cm$ angegeben, liefert die Formel das Ergebnis in $cm^2$.

Achtung! Sind a und b in unterschiedlichen Maßeinheiten angegeben, müssen Sie vor dem Einsetzen der Werte in die Formel durch Umrechnung dafür sorgen, dass a und b die gleiche Maßeinheit haben.

Beispiel: Volumen einer quadratischen Pyramide

Die Formel lautet: $V=\frac{1}{3} \cdot G \cdot h_k$. Sprich: „Ein Drittel mal G mal hk“.

Zunächst berechnen wir $G$. Da es sich um eine Pyramide mit quadratischer Grundfläche handelt, rechnen wir $G = a^2$, wobei $a$ die Seitenlänge der quadratischen Grundfläche ist. Den Wert für $G$ setzen wir dann in die Volumenformel für Pyramiden ein und berechnen das Volumen.

Dazu geben wir in den Taschenrechner ein: 1 geteilt durch 3 mal $G$-Wert mal $h_k$-Wert.

Wurden $a$ und $h_k$ in $cm$ angegeben, erhalten wir das Ergebnis in $cm^3$. Sind die Maßeinheiten verschieden, müssen wir sie zunächst durch Umrechnung angleichen (siehe oben, Rechteckbeispiel).

PDF Übung: „Kreis: Umfang und Fläche“
PDF Übung: „Kugel: Umfang, Fläche, Volumen“