Einfache Gleichungen

Was ist eine Gleichung?

Was eine Gleichung ist, machen wir uns an folgendem Rechenbeispiel klar.

Den Umfang eines Rechteckes berechnen wir mit folgender Formel:

$$ U = 2 \cdot a + 2 \cdot b $$

Oder in Kurzschreibweise:

$$ U = 2 a + 2 b $$

Ein Rechteck mit der Länge

$a=3~cm$

und der Breite

$b = 5~cm$

hätte den Umfang

$U = 2 \cdot 3 + 2 \cdot 5$

also $16~cm$.

Angenommen wir hätten ein Rechteck mit einem Umfang von

$U = 10~cm$

und einer Länge

$a = 2~cm$.

Wie breit wäre dieses Rechteck?

Auch hier hilft uns die obige Formel weiter. Wir setzen die bekannten Werte ein und erhalten:

$ \begin{matrix} 10 &=& 4 + 2 b\\ \end{matrix} $

So etwas nennen wir eine Gleichung. Da das Gleichheitszeichen festlegt, dass das auf seiner rechten Seite den gleichen Wert hat, wie das auf seiner linken Seite, können wir uns die Gleichung auch als Waage vorstellen.

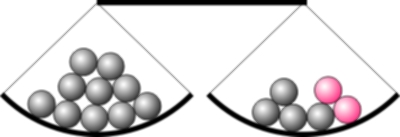
Die Waage bildet unsere Gleichung ab. In die linken Schale haben wir zehn schwarze Kugeln gelegt. In der rechten Schale liegen vier schwarze und zwei rote Kugeln. Insgesamt ist die Waage im Gleichgewicht.

Alle schwarzen Kugeln sind gleich schwer und alle roten Kugeln sind gleich schwer. Wieviele schwarze Kugeln entsprechen einer roten?

Um das herauszufinden, sortieren wir Kugeln in der Waage um, bis in einer Waagschale nur noch eine rote und in der andere Schale nur noch schwarze Kugeln liegen. Dabei achten wir darauf, dass die Waage immer im Gleichgewicht bleibt.

Wir nehmen aus der rechten Schale die 4 schwarzen Kugeln heraus. Damit die Waage nicht kippt, entnehmen wir auch der linken Schale vier schwarze Kugeln.

Für die Gleichung machen das auch. Hinter dem Protokollstrich auf der rechten Seite steht, was wir auf beiden Seiten der Gleichung tun: Wir ziehen 4 ab.

$ \begin{matrix} 10 &=& 4 + 2 b&|-4\\ 6 &=&2 b&\\ \end{matrix} $

Damit nur noch eine rote Kugel in der rechten Schale zurückbleibt, teilen wir die Anzahl der roten Kugeln in der rechten Schale durch zwei. Damit die Waage im Gleichgewicht bleibt, teilen wir die schwarzen Kugeln in der linken Schale ebenfalls durch zwei:

Und für die Gleichung:

$ \begin{matrix} 6 &=&2 b&| : 2\\ 3 &=&b&\\ \end{matrix} $

Eine rote Kugel wiegt also soviel, wie drei schwarze Kugeln.

In unserer ursprünglichen Überlegung ging es aber um ein Rechteck. Das ist demnach 3 cm breit.

Variable auf einer Seite

Rechenbeispiel:

$$ \begin{array}{rrcl} 3x&+9&=&30&|-9\\ 3x&~&=&21&|:3\\ x&~&=&7\\ \end{array} $$

Probe:

$$ \begin{array}{rrcr} 3x&+9&=&30&|x=7\\ 3\cdot 7&+9&=^?&30&~\\ 21&+9&=^?&30&~\\ ~&30&=&30&~\\ \end{array} $$

Variable auf beiden Seiten

Rechenbeispiel:

$$ \begin{array}{rrcll} 2x&+3&=&3x&-2&|-3x\\ -1x&+3&=&~&-2&|-3\\ -1x&~&=&~&-5&|:(-1)\\ x&~&=&~&5&~\\ \end{array} $$

Probe:

$$ \begin{array}{rrcrr} 2x&+3&=&3x&-2&|x=5\\ 2\cdot 5&+3&=^?&3\cdot 5&-2&~\\ 10&+3&=^?&15&-2&~\\ 13&~&=&~&13&~\\ \end{array} $$